One hundred years ago, in 1903, Joseph John Thomson, Professor of Natural Philosophy at Cambridge, published his classic, Conduction of Electricity Through Gases, based heavily on the coherence brought to his understanding of gaseous discharge by his work with Rutherford in 1896 on X-ray ionisatio of gases. Their joint paper brought together experimental results and mathematical theory in a close relationship unprecedented in the history of gaseous discharge. The theory they proposed was the, now seemingly straightforward one, that the X-rays dissociated the gas molecules into positive and negative ions, and subsequent recombination of the ions. The conductivity of the gas represented the number of ions free at any time.

What marked out Thomson and Rutherford's work and made it endure was the simple mathematical formulation, the good agreement between theory and experiment, and the power of the theory in assimilating other phenomena. Undoubtedly a number of factors were important in enabling the articulation between experiment and theory, in particular the new phenomena and techniques made possible by the discovery of X-rays. But in this paper I want to concentrate on the way the theory was formulated. What range of ideas and mathematical techniques did Thomson and Rutherford bring to their work and how did each man go about casting both their developing theory, and their experimental results, into mathematical form?

First I will examine the mathematical training of each man, and the way they put it into practice in articulating theory and experiment in some of their earlier work. Then I will discuss the work on X-rays, highlighting the contributions of each to formulating the theory.

J J Thomson

In 1896 J J Thomson was 40 years old. He had been educated primarily as a Cambridge Mathematician, graduating as 2nd wrangler (i.e. 2nd top) in 1880. Cambridge at the time was the centre of mathematical education in Britain, with an influence extending far beyond the university itself. To be a high wrangler (as the first class degree men were called) was a supreme intellectual distinction in Victorian Britain and great kudos attached to the school which had produced the senior wrangler (the top man).

Thomson's 'old school' was Owens College in Manchester, which he entered aged 14. Although he went to study engineering, his recollections show that he was sent to Owens partly because they had just produced a senior wrangler (John Hopkinson) ¹. And his maths teacher at Owens was Thomas Barker, himself a senior wrangler, who extended his teaching far beyond the standard schoolboy arithmetic and Euclid, lecturing on the logic of mathematics and on quaternions (Hamilton's system of geometrical analysis in which there was a revival of interest at the time). Barker recognised Thomson's potential and advised him to abandon engineering and try for a scholarship at Cambridge. Thus, even before entering Cambridge, Thomson's mathematical education was geared to the requirements of the Cambridge Mathematical Tripos.

At Owens Thomson was also greatly influenced by Osborne Reynolds, Professor of Engineering, and Balfour Stewart, Professor of Natural Philosophy. From Stewart, Thomson learnt the prevalent Victorian method of reasoning by analogy. Thomson's preferred analogies were always of vortices in the ether. Many factors at Owens contributed to this preference, among them Osborne Reynolds' experiments on vortices and his use of Rankine's textbooks, Balfour Stewart's adherence to vortex atoms and Arthur Schuster's lectures on Maxwell's electromagnetic theory. Rankine, in his textbooks, used vortex models extensively to explain thermodynamics. Equally important to Thomson were Reynolds' own research experiments in the 1870s on vortices. Like many Victorian physicists Thomson's mentors Stewart, Schuster and (indirectly) Maxwell, sought unification of knowledge in the ether which was thought to be the fundamental medium and the ultimate seat of all phenomena and Thomson followed suit, retaining his belief in the ether until his death in 1940.

Thus, even before he left Owens College and went to Cambridge at the age of 20 the major stylistic themes of Thomson's later work can be traced: the familiarity with advanced mathematics, the use of hydrodynamical analogies within an ether based physics, and the enthusiasm for research. These were reinforced by his intensive Cambridge training in the methods of analytical dynamics (the use of Lagrange's equations and Hamilton's principal of varying action).

By the 1870s analysis was central to the syllabus in the form of analytical geometry and dynamics and a system of coaching had grown up to prepare aspiring mathematicians for the increasingly competitive tripos exam. Thomson's coach, Edward Routh, was far and away the most important influence on his mathematical thinking. Routh was the most famous and successful of all Cambridge coaches. He had been senior wrangler in 1854. His original research was in analytical dynamics and he grounded his students thoroughly in its methods. Physical subjects taught included statics, dynamics, hydrostatics, optics and astronomy, Newtonian planetary motion and Electricity and Magnetism in the analytical mathematical form of Maxwell. But even in 1881 when Thomson took the Tripos, nine years after the founding of the Cavendish Laboratory, students were still discouraged from relating mathematical theory directly to experiment. The Cambridge mathematician, after years of intense coaching, viewed all physical processes as exercises in analytical dynamics.

An example from Thomson's early research shows this very clearly. Here Thomson is applying analytical dynamical methods to electromagnetism ². He defined any system using coordinates: x's for the position of bodies in the field, y's for the molecular configuration of bodies and z's for the electrical configuration. He then expressed the total kinetic energy (T) of the system in its most general form:

He considered each term in turn to see what type of phenomena they gave rise to because, 'if from any one phenomenon we get evidence of the existence of any of these terms, Lagrange's equations allow us to anticipate other phenomena'. For example, considering the term T_xy:
'The emf arising from this term is

( see 3 )

This will be zero unless this part of the kinetic energy involves the electric coordinates. If it does it '... will indicate an emf depending on the velocities of the bodies in the field, which will be reversed if the velocity of every body in the field is reversed.'

Lengstrom's experiments, in which a ring of insulating material rotating with high velocity acted like a galvanic current, gave some evidence for such a phenomenon, so Thomson went on to consider the implications:

'... the force tending to increase a molecular coordinate y is

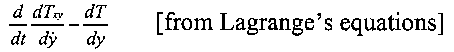
Therefore he suggested that in Lengstrom's experiment, if the ring was charged and the velocity of rotation increased, then the motion of the molecules in the ring would be altered, which would probably be shown by an alteration in temperature. However, his analysis gave no indication of the magnitude of such a temperature change.

This was a constant weakness of analytical dynamics. It could predict one phenomenon from another but, without a detailed model of the mechanism involved, it gave no indication of the size of effect to be looked for. This made direct quantitative comparison between theory and experiment virtually impossible. Thomson realised the importance of quantitative experimental results, but resorted to comparing general trends seeking, in his words, 'to get results whose magnitude admit of being compared roughly with theory' [my emphasis].

Rutherford

Superficially, Rutherford's education looks fairly similar to Thomson's but the details and context were completely different. Rutherford was born and educated in New Zealand until he came to Cambridge in 1895 at the age of 24. In New Zealand he attended, first Nelson College where he received a broad basic education, and later Canterbury College, Christchurch, part of the University of New Zealand.

As a scholar at Canterbury College, Rutherford had to attend lectures in at least four subjects each year, chosen from Latin, Greek, mathematics, higher mathematics, modern languages, English literature, jurisprudence or logic and moral philosophy, physical science, and natural science ⁴ . Thus Rutherford, although specialising in mathematics and science, did not study them intensively as Thomson had done. And throughout his university career, he concentrated equally on both, graduating in 1894 with first class honours in mathematics and also in physical sciences.

Like Thomson at Owens, Rutherford was taught mathematics by a Cambridge man. C H H Cook was 6th wrangler in 1872 and became professor of maths at Canterbury College a year later. But, unlike Thomson's teachers, Cook had been brought up in Australia and understood the colonial need for technical expertise. For the next 15 years he campaigned for a school of engineering. In 1885 science and mathematics courses were adapted to the need for technical education, and in 1887 a school of engineering was finally founded with Cook, professor of mathematics, heading it pending the appointment of a professor. It seems likely that Rutherford's mathematical education was far more grounded in practical problems than was Thomson's, although all we know of Cook's teaching is that it was 'able, sound and orthodox' ⁵.

It is clear from Rutherford's early papers and the books he read that, although no mathematician in the Cambridge sense, he was well grounded in calculus, performing standard integrals and linear differential equations as a matter of routine, and could at least follow potential theory, Gauss' theorem, Green's theorem, etc. At this level he quite confidently applied maths to science, which he learnt from Alexander William Bickerton.

Bickerton, like Thomson's teacher Balfour Stewart, was an inspiring teacher and an enthusiast for research, but there the similarity ended. Balfour Stewart's background was mainly in pure science and an ether-based physics. Bickerton, on the other hand, had had a varied career in applied science. He was a graduate of the Royal School of Mines who had been a railway engineer, been Hampshire county analyst, and taught technical classes, before going to Canterbury College in 1873. He had a gift for public demonstration and his courses on applied science and applications of electricity at Canterbury College attracted large audiences ⁶.

Thus, it seems that in science as well as in mathematics, the philosophy of Rutherford's education was practical. He was taught to test his experiments against prevailing theories and to devise theories which made definite practical predictions. This was shown in his first original work on the magnetic viscosity of iron, and the magnetisation of iron in rapidly changing fields, topics which had practical implications for the design of transformers etc. ⁷ Looking at this work, three important points are apparent:

1. Rutherford's was not an ether-based physics, and he was virtually ignorant of Maxwellian theory. Although he relied heavily on Thomson's Recent Researches in Electricity and Magnetism and Lodge's Modern Views of Electricity he totally ignored the ethereal and Maxwellian aspects and focussed on the practical implications. He used a number of equations from Thomson's Recent Researches, but only those couched in measurable experimental parameters. This forms a contrast to Thomson who, as we have seen, was often led by Maxwellian electrodynamics far beyond the realms of practical possibility.
   
   
2. Rutherford had evidently been taught to relate mathematical formulae very directly to quantitative experimental results by means of graphs, a complete contrast to Thomson who scarcely ever used curves in his own work. Rutherford's notebooks show that his first recourse on obtaining a set of data was to plot a curve for them, often with the theoretical curve sketched in also. He used this technique to compare experiments with pre-existing theory, to generate formulations of his results, and to extrapolate his data.

   The origin of Rutherford's reliance on graphical methods is unclear, but probably lies in Bickerton's teaching of applied science and in Rutherford's chosen subject matter. As well as Thomson and Lodge, Rutherford based his work on Ewing's Magnetism, Fleming's Alternate Current Transformer and Gray's Absolute Measurements. Curve plotting was a standard technique in these more applied works, particularly in discussions of magnetic hysteresis.

3. in his work on magnetic viscosity Rutherford acquired an important theoretical concept, that of the equilibrium between opposing forces, for instance in the time of rise of current in a coil of known self inductance or reversals of magnetisation in changing fields. This idea was to recur again and again in Rutherford's work: on ionisation of gases, in separation of radioactive products, and in determining radioactive decay series. The equilibrium concept was to Rutherford what ethereal vortices were to Thomson.

Largely on the basis of this work on magnetism Rutherford was awarded an 1851 Exhibition Scholarship to go to the Cavendish. Bickerton's recommendation should be taken very seriously: 'Mr Rutherford has ... a very full acquaintance with both the analytical and graphic methods of mathematics and a full knowledge of the recent advances in electrical science and methods of absolute measurement.' ⁸

The collaboration on X-ray ionisation

At the beginning of April 1896 Rutherford had been at the Cavendish for six months, X-rays had been discovered five months previously, and Thomson had been investigating them for three months.

Thomson's work was on two fronts, the mathematical/theoretical investigations of whether X-rays might be longitudinal ether waves, and the experimental/qualitatively theoretical work on the discharge of electrified bodies by X-rays, some in collaboration with J A McClelland.

When Thomson invited Rutherford to join him it was not just because he wanted a gifted experimentalist but, very specifically, he wanted someone with practical skills in high frequency electrical experiment to elucidate a theoretical question - whether the ether could be set in motion by a varying electromagnetic field. This was a necessary condition for the existence of longitudinal electromagnetic waves ⁹.

This initial experiment has been entirely overlooked, largely because the results were negative and Rutherford himself dropped the subject as soon as possible. Thus, while Thomson, in September 1896, stated that the experiments were not yet complete, and eventually persuaded W C Henderson and J Henry to pursue them, Rutherford had already reported in May to the Commissioners of the 1851 Exhibition that, 'so far as the experiment goes it proves there is no movement of the ether in the neighbourhood of a vibrator,' adding that, 'the method is of course capable of detecting a very minute actual movement of the ether.'¹⁰ He never mentioned the experiment again. It had confirmed his non-ethereal approach to physics, but provided his entrée into X-ray research where he rapidly became central to Thomson's experimental programme. While Thomson continued to devote much of his attention to the more fundamental, but less experimentally tractable, question of the nature of X-rays, Rutherford chose to concentrate on the experimental effects they produced.

Thomson approached the collaboration with a range of theoretical preconceptions about gaseous conductivity and some important experimental skills, while Rutherford had almost none - this was a totally new field for him and he had to learn afresh. Inevitably, the work initially reflects Thomson's methods and concerns. But increasingly, as Rutherford found his feet, he took control.

Since 1890 Thomson had believed that gaseous conductivity was due to the dissociation of molecules made up of oppositely charged atoms, bound together by 'Faraday tubes' of electrostatic induction which he thought of as vortices in the ether. A further development was his suggestion of chain type aggregates, which he called Grotthus chains, in the gas. These would weaken the molecular bond and lower the energy of dissociation and would form a conductor down which a discharge could pass with a velocity approaching that of light.

Thomson worked this theory out in great mathematical detail in Recent Researches, analysing the energy and momentum of the Faraday tubes, but was unable to make any quantitative predictions from it, or to isolate any experimentally measurable parameters, because he lacked evidence of how the tubes interacted with material atoms ¹¹. Despite this, the theory guided most of his work on X-ray ionisation.

He also brought two important experimental discoveries to the collaboration. The first was that X-rays discharge an electrified plate on which they fell by, he supposed, turning the surrounding gas into a conductor. He rapidly turned this into a quantitative technique, and almost all his later experiments on X-ray ionisation used the method. The rate of leak of charge from the plate was used to measure the intensity of X-rays and to monitor the output of the X-ray tubes, or alternatively to measure the conductivity of the gas.

Secondly, Thomson and McClelland reported in March that with increasing potential of the leakage plate, the rate of leak and the current rapidly increased to a maximum value and thereafter remained steady. It became 'saturated'.

Thomson interpreted the saturation current by analogy to the magnetisation curve for iron. He postulated that X-rays produced chains of molecules in the gas along which electricity could pass, as with the Grotthus chains. Generally the chains were randomly oriented, but between electrified plates the chains aligned themselves and a net current flowed. The maximum current was reached when all the chains were aligned.

Although Thomson had these quantitative techniques, he lacked a theory to fit them to, other than by analogy.

The main source of information about the further progress of Thomson and Rutherford's collaboration is a notebook covering the period from 9 July 1896 onwards ¹².

It opens with a series of experiments to establish the conditions of experimental geometry, pressure etc, under which the current became saturated. They had found that the saturation current increased with the distance between the plates, i.e. the resistance of a thin layer of gas was higher than that of a thick layer. This fitted Thomson's preconceptions well. If conduction was by long chains of molecules, it was reasonable to suppose that in a confined space the chains were not able to align themselves or function efficiently, leading to a high resistance. Thus these experiments investigated aggregate formation and conductivity. Despite a mass of quantitative results no advances were made as there was still no way of linking the mathematical theory directly to experiment.

Then came a break, and a change of direction. A new page was started in the notebook and a new apparatus described. They took the significant step of blowing the conducting air down a tube before investigating its conductivity, thus isolating it from its source of conductivity, and the first things they investigated were the ways the conductivity could be destroyed (rather than, as hitherto, how it was produced). Was this where Rutherford, with his favoured interpretation of phenomena as an equilibrium between opposing forces, took a hand? Probably, for the first experiment entered in detail was to look at the effect of inserting an electrified wire down the centre of the tube.

After only a couple of runs of the experiment they concluded:

'The effect of having a high potential wire around which Roentgenised air is passing is therefore to rob the air of its property of discharging another plate almost completely. From the large difference in the effect obtained at the end of the long tube, it looks as if, the whole of the molecules which are split up by the rays are used up in the passage of the leak from the high potential wire to the side.'¹³

They added, significantly,

This was not added as an afterthought; it is an integral part of the text. The explanation was characteristic of Rutherford: the saturation current represented a balance between the creation of ions by the X-rays and their destruction by the current itself. They had clearly realised this possibility even before performing the experiment and the reinterpretation of saturation current, which allowed a mathematical formulation of their results, had been conceived of before the crucial experiment which made it possible.

Rutherford had abandoned a theoretical approach which, while it had a mathematical form, was incapable of relating to experiment, and sought instead a level of theory at which he could make direct experimental comparisons. Thus he abandoned Thomson's speculations about the nature and production of ions and concentrated on measuring their observable properties. More specifically, he recognised and seized upon properties which could be cast into a form he was already familiar with, that of a equilibrium equation:

In a steady state dn/dt is zero, so

(1)

He used this equation to match various parts of the current curve. When the current is small it gives

hence the number of conducting particles is independent of the current, and the current will be proportional to the emf, corresponding to the straight part of the curve.

In general, though, the current is proportional to n times the potential gradient E/l . Thus if U is the sum of the velocities of the positive and negative ions when the potential gradient is l , then

Substituting this value into equation (1) gives

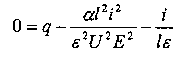
As the potential E increases, i approaches a limit of

the saturation current.

This was a step of outstanding significance to Thomson. Having at last achieved a mathematical formulation for gaseous conductivity, he and Rutherford rapidly assimilated other phenomena. They repeated all their saturation current measurements and plotted curves of the results. They used these to estimate the fraction of dissociated molecules in the gas (about 1/3x10¹²), to explain why a thin layer of gas had higher resistance than a thick layer (there were fewer free ions) and to estimate the velocity of the ions.

The ionisation theory proved to be a general theory which explained many of the phenomena of the discharge tube, and by 1901 was so well established that the Curies termed it 'classic' when they wrote nominating Thomson for a Nobel Prize¹⁴. Arrhenius, reporting on Thomson's work to the Nobel Prize committee thought this was his 'greatest achievement' and wrote that:

'By building on the principles he achieved through the study of ionised gases, Thomson has formulated a theory which includes all cases of electrical conduction through gases.... Our knowledge of the nature of electricity has made a greater advance... in particular through the work of Thomson, than through all previous developments in this area.' ¹⁵

Conclusion

In the X-ray work we see two men, with very different mathematical training, wrestling with the same phenomena. Thomson was an advanced mathematician, well able to formulate a mathematical theory in considerable detail and fully conscious of the value of quantitative experiment. Yet due to the nature of his Cambridge training, he was unable to match the two. In seeking a fundamental, ether based theory, he was missing the vital link of the interaction between the ether and matter which would allow him to relate theory directly to experiment.

Rutherford, while clearly a competent mathematician, was much better grounded in practical science. He had been taught to relate theory directly to experiment by curve matching and if a fundamental theory did not have quantitative experimental implications he abandoned it and sought a less fundamental one which did. It was not pure luck that in X-ray ionisation he found phenomena which could be cast into a mathematical form with which he was familiar; he was actively seeking some such parameters.

Rutherford's work can be characterised as the steady and certain advance of theory through experimentally well justified steps. Nine years later, apropos radioactivity, Larmor wrote to Kelvin, 'The way that Rutherford feels his path through all these mazes without once having to withdraw anything seems to me very wonderful'. ¹⁶ In the case of ionisation, this approach paid clear dividends. But this is not to write off Thomson's alternative methods. Thomson's work was a series of wild theoretical guesses, matched only in general terms to experiment: guesses which he frequently had to retract, and did so without embarrassment. Occasionally he was right, as in the case of the electron the following year; a discovery which, I suggest, Rutherford is unlikely ever to have made.¹⁷

References

• 1 Thomson, J.J. 'Recollections and Reflections' (1936) p15
• 2 Thomson, J.J. 'On Electrodynamics'. MS of Fellowship thesis. Cambridge University Library ADD 7654 UD3 from which the quotations in this account are taken.
• 3 Christopher Green has pointed out that the partial derivative symbol '_' we would normally use here was probably unknown to Thomson as it was not generally used until 1890's. I am indebted to him for this information.
• 4 Hight, J. & Candy, A. 'A Short History of Canterbury College' (1927) pp 26- 27.
• 5 Jenkinson, S.H. 'New Zealanders and Science' (1940)
• 6 ibid
• 7 Rutherford E. 'Magnetization of Iron by High Frequency Discharges' Transactions of the New Zealand Institute 27 (1894) 481-513; 'Magnetic Viscosity' Transactions of the New Zealand Institute 28 (1895) 182-204
• 8 Eve, A.S.'Rutherford' p12
• 9 Thomson, J.J. 'Longitudinal Electric Waves and Rontgen's X-rays' Proceedings of the Cambridge Philosophical Society 9 (1896) 49-61
• 10 Rutherford E. 'Report to the Commissioners of the 1851 Exhibition' 30 May 1896. Archives of the 1851 Exhibition, file 78
• 11 Thomson J.J. 'Notes on Recent Researches in Electricity and Magnetism' (1893)
• 12 Rutherford E. 'Notebook' Cambridge University Library ADD 7653 NB3
• 13 ibid. f15
• 14 Curie, M. & P. 'Letter Nominating Thomson for the Nobel Prize' (1905) Nobel Archives
• 15 Arrhenius, S. (1906) 'Justification by the Nobel Committee for Physics of their proposed award for the 1906 prize' Nobel Archives, Stockholm, 16ff, f14 translation from the Swedish by Karin Morgan
• 16 Larmor to Kelvin, Cambridge University Library ADD 7342 L38
• 17 see Davis, E.A. and Falconer, I. J. 'J.J. Thomson and the Discovery of the Electron' (1997) for the speculative nature of Thomson's work on the electron

Next     Top